데드락, 뭔가 이름부터 무시무시하다.
한국어로는 '교착상태' 라고 한다.
수업시간에 교수님께서 그렇게나 이 개념을 강조하셨다.
발생 조건이 뭔지 짚어보기 전에, 데드락의 개념을 쉽게 이해하기 위해 다음의 상황을 생각해본다.
프로세스 1 (P1) 이 작업을 수행하려면 자원 A, B 가 필요하다고 하자. 이때, P1 은 A를 갖고 있다.
프로세스 2 (P2) 가 작업을 수행하려면 자원 A, B 가 필요하다고 하자. 이때, P2 은 B를 갖고 있다.
P1은 P2가 작업을 수행하고 B를 반환하기를 대기하고 있다.
P2는 P1이 작업을 수행하고 A를 반환하기를 대기하고 있다.
>> 서로가 서로를 기다리며 무한 대기상태에 빠진다. 이를 교착상태라고 한다.
생각보다 간단하네.
결국 유한한 자원을 두고 여러 프로세스가 경쟁하며 발생하는 현상인 것이다.
교착상태는 다음의 조건이 동시에 성립할 때 발생한다.
- Mutual Exclusion (상호 배제)
: 프로세스들이 사용하는 여러 종류의 자원 중 적어도 하나는 한 번에 한 프로세스만이 해당 자원을 사용할 수 있어야 한다. - Hold and wait (점유 대기)
: 적어도 하나의 자원을 갖고 있는 (holding at least one resource) 프로세스는, 프로세스를 실행하는 데에 있어 필요한 다른 자원들이 (다른 프로세스들에 의해서) 사용중이라면 점유중인 자원을 들고 대기한다. - No preemption (비선점)
: 자원은 강제로 반환될 수 없고, 해당 자원을 점유중인 프로세스가 필요한 작업을 끝마친 후에 자발적으로 반환한다. 어떠한 자원도 특정 프로세스가 선점할 수 없다. 특정 프로세스가 자원을 '선점'하여 다른 프로세스로 하여금 점유중인 자원을 강제로 반환하게 할 수 없다는 의미에서 'No preemption'인 것으로 이해했다. - Circular wait (순환 대기)
: 프로세스의 집합 {P0, ... Pn} 이 있다고 하자. 이때, 모든 Pk-1이 Pk 가 사용중인 자원을 사용하기 위해 대기하고 있는 경우, 순환대기가 발생한다. (단, 1≤ k ≤n이고, Pn은 P0이 사용중인 자원을 사용하기 위해 대기하고 있다) 쉽게 생각해서, 꼬리에 꼬리를 물고 원을 그리며 서로를 대기하고 있다고 생각하면 된다.
교착상태는 그래프로 표현해볼 수 있다.
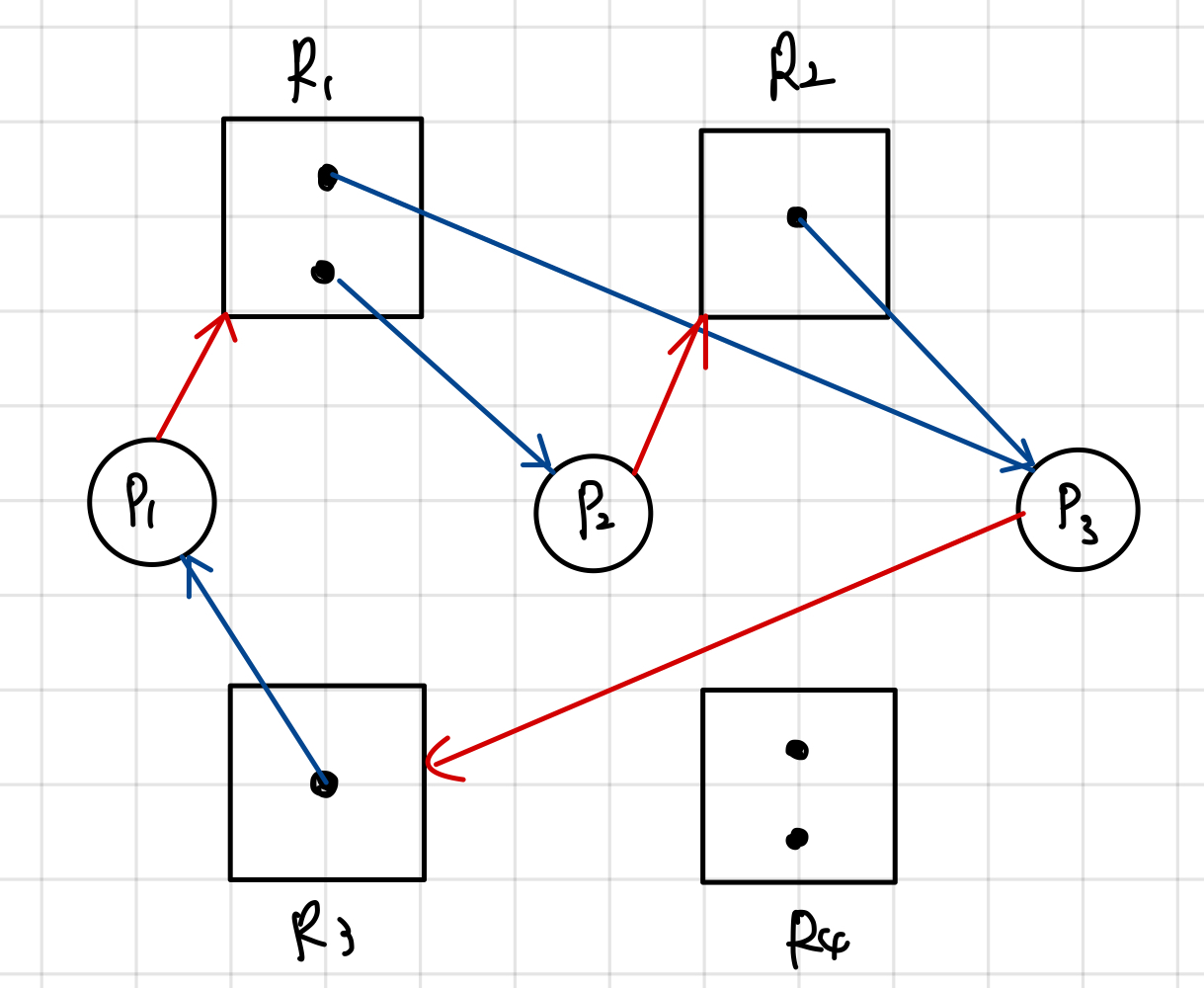
위 그림에서는 자원의 종류당 여러 개의 인스턴스가 있는 경우를 나타내기 위해 '점'을 여러개 찍어두었다.
사실 그래프를 그렸다면 그래프를 구성하는 Vertex, 그리고 Edge에 대한 정의를 명시해두어야 한다.
(Pi (i=1,2,3), 으로부터 Rj(j=1,2,3,4)로의 directed edge는 무엇이고 그 반대의 경우는 무엇이고, 해당 edge를 무엇이라 명명하고 등등)
하지만 직관적인 이해를 돕기 위한 '그림' 차원에서 그려둔 것이고, 학술적으로 정의하지 않았을 뿐 위에 설명한 것으로 충분히 의미는 통할 것이라 믿기에 글의 복잡성을 높이지 않는 차원에서 그 부분은 생략하겠다.
다음의 개념을 알아둔다면 그래프로 나타낸 프로세스 자원 분배에서 직관적으로 교착상태를 파악 할 수 있다:
- 그래프에 사이클이 존재하지 않는 경우
>> 교착상태 없음 - 그래프에 사이클이 존재하는 경우
a) 자원 당 하나의 인스턴스가 있는 경우
>> 교착상태
b) 자원 당 여러개의 인스턴스가 있는 경우
>> 교착상태일 가능성 있으니 확인 필요
#이산수학_그래프_사이클
한창 수능 공부를 할 때, 국어 비문학 제시문에서 단골로 출제되는 제시문 유형이 있었다.
바로 Problem and Solution 유형 (내가 지은 이름).
이름에서 알 수 있듯이, '특정 문제 상황을 인지했을 때, 그것에 대한 해결책으로 무엇을 했는가에 대한 논리적인 흐름을 읽을 수 있는 경우' 나는 Problem and Solution 유형이구나! 라고 생각하고 문제를 풀었던 기억이 난다.
공부를 하면 할 수록 느끼지만, 특히 공학계열 전공 공부는 '문제상황 인식과 그 해결책 연구'를 어떻게 했나 공부하는 것의 반복인 것 같다.
대학원에 진학하는 것은 직접 문제상황을 찾아서 인식하고 그 해결책을 연구해 볼 수 있는 기회를 잡기 위함이라고 보면 될 것 같다.
실제로 연구실 경험을 해보니 더더욱 그렇게 느껴진다.
이번 게시글에서는 Deadlock이 어떤 Problem인지 알아보았다.
다음 게시글에서는 Deadlock을 인지한 후, 앞선 과학자들께서 제시한 Solution 들에 대해 알아보겠다.
*오개념 지적 대환영*
#키워드 : (게시글이 있는 경우) 링크를 참고하시거나, 검색하면서 읽어주세요. 이해에 꼭 필요한 개념입니다.
해당 게시글은 Operating Systems: Three Easy Pieces(#혜성책), Operating System Concepts (#공룡책), 그리고 이 도서를 기반으로 한 학부 수업 자료를 참고하여 작성하였습니다.
'CS > Operating Systems' 카테고리의 다른 글
| OS_Contiguous Allocation(Fragmentation) (0) | 2020.12.06 |
|---|---|
| OS_Deadlock(3): Solution(Prevention and Avoidance -Banker's Algorithm) (0) | 2020.11.30 |
| OS_Deadlock(2): Solution(Detection and Recovery) (0) | 2020.11.30 |
| OS_Swapping (0) | 2020.11.28 |
| OS_Main Memory (0) | 2020.11.27 |